Инновации 24 июня 2021

Кривая чемпионского класса

Российские специалисты предложили инновацию мирового уровня в геометрическом моделировании. Сотрудники компании — национального чемпиона создали новый класс кривых, которые до сих пор не были описаны. С их помощью можно совершенствовать самые разные устройства — от плуга до лопатки газовой турбины

Модель плуга в системе «Компас-3D»

Пресс-служба C3D Labs

В инженерную геометрию вводится термин «функциональные кривые», или «кривые класса F». Разработка методов моделирования кривых класса F значительно расширяет возможности моделирования поверхностей, к примеру в авиа-, автомобиле- и судостроении. C3D Labs — дочерняя компания лидера российского рынка САПР, компании АСКОН, которая недавно стала еще одним национальным чемпионом.

Идея создания функциональных кривых принадлежит кандидату технических наук Валерияну Муфтееву. Он опубликовал цикл научных работ по этой теме. С 2019 года Муфтеев работает в C3D Labs, и его теоретические исследования нашли применение в геометрическом ядре C3D.
«Сотрудничество началось по моей инициативе, — рассказал “Стимулу” Валериян Муфтеев. — Как сертифицированный преподаватель САПР, я хорошо знал систему автоматизированного проектирования “Компас-3D”. Я и тогда понимал, и сейчас понимаю, что мои разработки могут вывести систему на совершенно другой уровень, сделать ее лучшей в мире. И написал письмо в АСКОН — предложил мою идею, но мне не ответили. Я немного подождал и написал еще раз».

Идея создания функциональных кривых принадлежит кандидату технических наук Валерияну Муфтееву

Пресс-служба C3D Labs

И после второго письма руководство С3D Labs обратило внимание на идеи Валерияна Муфтеева, потому что в тот момент было принято стратегическое решение начать развивать геометрическое ядро C3D в сторону сложного поверхностного моделирования для авиационной и судостроительной отраслей. «Ученого пригласили выступить перед нашей командой, — рассказал “Стимулу” директор С3D Labs Олег Зыков, — на лекции присутствовали и аналитики материнской компании АСКОН, которая занимается разработкой программы “Компас-3D”. Оказалось, что все сходится, это действительно то, что нам нужно. И тогда, в 2019 году, мы начали совместную работу».

Самые жесткие требования

Среди функциональных кривых можно выделить подкласс инженерных аналитических кривых, которые единственным оптимальным образом обеспечивают некоторую проектную характеристику объекта. К таким кривым, например, можно отнести эвольвенту окружности, используемую для построения профиля зубьев зубчатого колеса, а также брахистохрону — кривую наискорейшего спуска для транспортировки предметов.

В остальных случаях функциональные кривые имеют свободную форму. Такие кривые могут быть локально-выпуклыми (с постоянным знаком функции кривизны) и иметь точки перегиба (участки с разным знаком функции кривизны). Кроме того, функциональные кривые могут быть пространственными и, соответственно, иметь кручение.

Функциональные кривые принципиально отличаются от обычных гладких кривых по многим критериям. К параметрам плавности рассматриваемых инженерных кривых предъявляются повышенные требования. Эти требования универсальны и не зависят от специфики проектируемых объектов. Кривые оценивают по порядку гладкости, числу экстремумов кривизны, вариации кривизны и скорости ее изменения, потенциальной энергии кривой, а также с точки зрения технической эстетики.

Порядок гладкости требуется не ниже четвертого. Гладкость — это свойство функции или геометрической фигуры (кривой, поверхности и др.), определяющее, дифференцируема ли функция на всем множестве определения или имеется ли у каждой точки данной фигуры окрестность, допускающая задание с помощью дифференцируемых функций.

Функциональная кривая должна иметь минимальное число экстремумов кривизны на фиксированных исходных данных вида опорной ломаной или касательной ломаной. Плавность кривой также зависит от формы графика изменения кривизны вдоль линии движения. Наличие лишних экстремумов кривизны, например, у формы технических изделий и объектов дизайна может вызвать следующие негативные явления:

— неоправданное биение толкателя кулачкового механизма, следствие — преждевременный износ механизма;

— залипание почвы на участке плуга с концентрацией кривизны у траектории движения почвы, что приводит к увеличению сопротивления плуга и повышению энергоемкости процесса вспашки;

— при лишних экстремумах кривизны на аэродинамическом профиле — неоправданная пульсация среды, обтекающей профиль, что увеличивает его лобовое сопротивление и может спровоцировать срыв потока;

— необходимость лишних торможений и разгонов, что увеличивает энергозатраты на перемещение по трассе транспортного средства;

— эффект кривых зеркал у кривых кузовных поверхностей и архитектурных форм;

— неправильное визуальное восприятие объектов компьютерной графики и CAD.

В некоторых прикладных областях вводится требование минимизации вариации кривизны, следовательно, концентрация кривизны должна быть ограничена по максимальному значению. Например, такое ограничение минимального значения радиуса кривизны (максимальной кривизны) естественным образом вводится при проектировании дорог: минимальный радиус виража ограничивается из расчета допустимой скорости транспортного средства.

Важным параметром качества кривой является скорость изменения кривизны. При проектировании трассы дороги этот параметр регламентирует скорость нарастания центробежной силы, действующей на автомобиль на виражах, и легко контролируется благодаря применению сегментов клотоиды с линейным изменением функции кривизны.

Считается, что плавность кривой напрямую связана с ее потенциальной энергией. Необходимость выбора функциональной кривой с малым значением потенциальной энергии основывается на предположении, что при движении объекта с функциональной поверхностью с большой скоростью среда, обтекающая объект, ведет себя как упругое тело. Очевидно, что для деформации упругой среды по линиям тока с меньшей потенциальной энергией будет затрачиваться меньшая работа. При движении материальной точки по вогнутой криволинейной траектории с учетом трения работа, затрачиваемая на перемещение, будет меньше при меньшем значении потенциальной энергии траектории перемещения.

Помимо предложенных выше объективных критериев плавности качество кривой при проектировании изделий промышленного дизайна необходимо оценивать с позиций законов технической эстетики. Существует такой подход к оценке эстетичности кривой, когда форма кривой базируется на математических характеристиках форм, выявленных у объектов реального мира (например, очертания крыльев бабочек).

Без CAD-систем никуда

В современном мире CAD-системы, позволяющие моделировать поверхности сложных форм, востребованы повсеместно. Их возможности задействованы при решении многих проектных задач в самых разных областях науки и техники. Однако даже если CAD-система поддерживает моделирование кривых и поверхностей класса А, она не обеспечивает надлежащего качества так называемых функциональных кривых по критериям плавности.

Руководство С3D Labs обратило внимание на идеи Валерияна Муфтеева, потому что в тот момент было принято стратегическое решение начать развивать геометрическое ядро C3D в сторону сложного поверхностного моделирования для авиационной и судостроительной отраслей

Перед разработчиками C3D Labs встала задача реализации такого функционала, который позволил бы моделировать кривые линии и, соответственно, поверхности самого высокого качества. В результате проведенных изысканий в области геометрического моделирования на свет появился C3D FairCurveModeler — новый раздел геометрического ядра C3D Modeler, позволяющий строить кривые класса F.

К новому типу кривых относятся плоские и пространственные кривые, которые обеспечивают некоторую функциональную характеристику объекта, в связи с чем их целесообразно называть функциональными кривыми.

«У нас в ядре появился функционал, который строит плавные кривые, имеющие минимальные изменения кривизны, — пояснил “Стимулу” руководитель разработки C3D Labs кандидат технических наук Николай Голованов. — Доказать это можно следующим образом: если вершины ломаной лежат на окружности произвольно, разбросаны по окружности, и по ним нужно провести плавную кривую, то с помощью этого метода она приобретает форму окружности. То есть мы достигаем нужной нам цели — минимального изменения кривизны, ведь у окружности она не меняется. А в произвольном случае, когда мы строим некую кривую по набору точек, то получается плавная кривая, которая минимально меняет свою кривизну, и, соответственно, имеет минимальную потенциальную энергию. Такие кривые оказались очень востребованы, к примеру, в авиации, автомобилестроении. По этим кривым строятся плавные поверхности. И физические свойства таких поверхностей — наилучшие».

Руководитель разработки C3D Labs кандидат технических наук Николай Голованов

Пресс-служба C3D Labs

Область применения функциональных кривых весьма широка и распространяется в основном на проектные задачи, возникающие в разных отраслях техники. Например, задача максимизации подъемной силы при минимизации лобового сопротивления при моделировании профиля крыла самолета или задача поиска максимальной плавности трассы при заданных ограничениях для обеспечения комфортной и безопасной езды на транспортном средстве. С их помощью можно даже усовершенствовать плуг.

Идеальная вспашка

Обычно при оптимизации конструкции берется некоторый приоритетный параметр, который минимизируется (максимизируется), при этом остальные параметры ухудшаются. Грамотная оптимизация заключается в том, чтобы остальные параметры остались в пределах некоторых ограничений. Один из наиболее ярких примеров применения функциональных кривых — моделирование плуга. Чтобы плуг лучше рыхлил землю, на него монтируются так называемые акульи плавники, но при этом неминуемо растет сопротивление плуга и, соответственно, расходы на горючее для трактора.

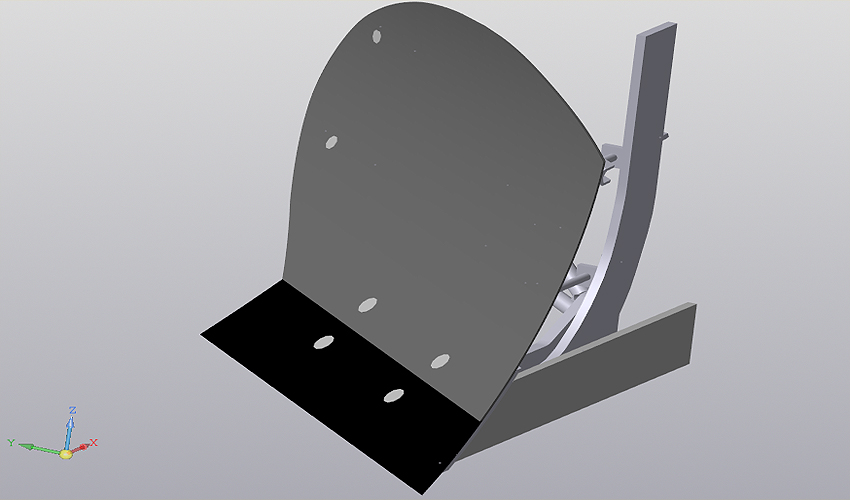
Была разработана прикладная программа, которая рассчитывает рабочую поверхность плуга. Аспирант отправился к себе в деревню, в кузницу, ему там сделали лекала. По этим лекалам изготовили плуг, испытали его, и получился поразительный результат

«В 2005 году я пошел преподавать в Башкирский государственный аграрный университет и на кафедре механизации предложил сделать им хороший плуг, — рассказывает Валериян Муфтеев. — В учебниках посмотрел стандарты. Мне дали аспиранта, и я его консультировал по геометрической части. В конструкции рабочей поверхности плуга есть направляющая кривая, и ее сделали параболой. Парабола имеет концентрацию кривизны, и там, как ни крути, будет залипание почвы, кривая получается некачественная. И мы туда встроили фрагмент клотоиды, который полностью соответствует стандартным макропараметрам плуга, с минимальной потенциальной энергией».

Помимо объективных критериев плавности качество кривой при проектировании изделий промышленного дизайна необходимо оценивать с позиций законов технической эстетики

«Обычно, когда улучшают, стараются одно улучшить, но за счет того, что другие параметры портятся, — поясняет Валериян Муфтеев. — Ставят “акулий плавник”, он хорошо рыхлит почву, но солярки тратится много. И в экономическом обосновании пишут: потеря на солярку — столько-то, зато урожай — столько-то. И за счет того, что продали больше, окупились потери солярки. А здесь получилось, что и почва лучше, и солярки нужно меньше».

По аналогии с подходом к оптимизации конструкции плуга в C3D Labs провели эксперимент по улучшению геометрии лопатки паровой турбины и получили улучшенные показатели средней скорости и общего давления.

Как пояснили в компании, функциональные кривые уже реализованы в геометрическом ядре C3D, и на их основе можно создавать программные продукты САПР для моделирования самых сложных поверхностей. Использование C3D FairCurveModeler — быстрый и недорогой способ улучшить проектные характеристики, поскольку качество изделия можно существенно повысить только за счет улучшения плавности его геометрии.

Темы: Инновации